Question

Don’t know how to solve with the -1 before the x

Answer 1

ANSWER and EXPLANATION

We are given a function and its inverse function:

`\begin{gathered} f(x)=(1)/(2)x \\ f^(-1)(x)=2x \end{gathered}`

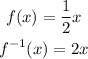
To solve the problems, we have to substitute the values of x in the brackets into the appropriate function (or inverse function).

Therefore, we have that the value of the function for x = 2:

`\begin{gathered} f(2)=(1)/(2)\cdot2 \\ f(2)=1 \end{gathered}`

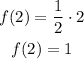
For x = 1, we have that the value of the inverse function is:

`\begin{gathered} f^(-1)(1)=2(1) \\ f^(-1)(1)=2 \end{gathered}`

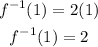
For x = -2, we have that the value of the inverse function is:

`\begin{gathered} f^(-1)(-2)=2\cdot-2 \\ f^(-1)(-2)=-4 \end{gathered}`

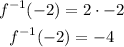
For x = -4, we have that the value of the function is:

`\begin{gathered} f(-4)=(1)/(2)\cdot-4 \\ f(-4)=-2 \end{gathered}`

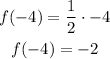
For the fifth option, substitute the value of the function at x = 2 into the inverse function.

That is:

`\begin{gathered} f^(-1)(f(2))=f^(-1)(1)=2\cdot1 \\ f^(-1)(f(2))=2 \end{gathered}`

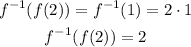
For the sixth option, substitute the value of the inverse function at x = -2 into the function.

That is:

`\begin{gathered} f(f^(-1)(-2))=f(-4)=(1)/(2)\cdot-4 \\ f(f^(-1)(-2))=-2 \end{gathered}`

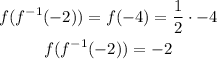
To find the general form of the function:

`f^(-1)(f(x))=f(f^(-1)(x))`

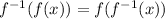
either substitute the function for x in the inverse function or substitute the inverse function for x in the function.

Therefore:

`\begin{gathered} f^(-1)(f(x))=2((1)/(2)x)) \\ f^(-1)(f(x))=x \end{gathered}`

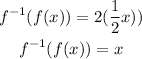
That is the answer.