ANSWER and EXPLANATION
We are given a function and its inverse function:

To solve the problems, we have to substitute the values of x in the brackets into the appropriate function (or inverse function).
Therefore, we have that the value of the function for x = 2:
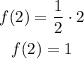
For x = 1, we have that the value of the inverse function is:
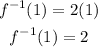
For x = -2, we have that the value of the inverse function is:
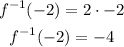
For x = -4, we have that the value of the function is:
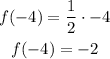
For the fifth option, substitute the value of the function at x = 2 into the inverse function.
That is:
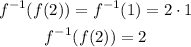
For the sixth option, substitute the value of the inverse function at x = -2 into the function.
That is:
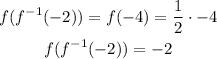
To find the general form of the function:
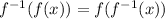
either substitute the function for x in the inverse function or substitute the inverse function for x in the function.
Therefore:
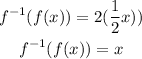
That is the answer.