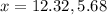Answer:
Form:
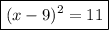
Solution:
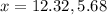
Step-by-step explanation:
Step 1. The expression we have is:
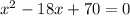
And we are required to find the appropriate form after completing the square, and then the solution or solutions to the equation.
Step 2. Compare the given equation with the general quadratic equation:

Our values for a, b, and c are:
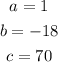
Step 3. Using the value of b, find the following expression:
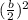
The result is:

Step 4. Take the original equation
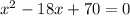
Move the +70 as a -70 to the right-hand side:
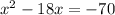
And now add to both sides the expression found in step 3 for (b/2)^2:
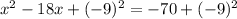
Step 5. Factor the left-hand side of the equation as a perfect square binominal:
![\begin{gathered} P\operatorname{erf}ect\text{ square binomial formula:} \\ (a\pm b)^2=a^2\pm2ab+b^2 \end{gathered}]()
Applying this to our expression:
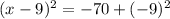
Step 6. Solve the operations on the right-hand side:
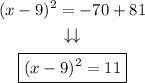
The form is the equation is:
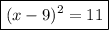
Step 7. To find the value or values of x, solve for x in the previous equation:
![\begin{gathered} (x-9)^2=11 \\ \downarrow\downarrow \\ x-9^{}=\pm\sqrt[]{11} \\ \downarrow\downarrow \\ x^{}=\pm\sqrt[]{11}+9 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/eeq1xnqiwfadidyl32h5xjsec70nk0h2lv.png)
Step 8. To find the two solutions we use the '+' and '-' signs separately:
![\begin{gathered} x^{}=\sqrt[]{11}+9\longrightarrow x=3.3166+9=12.3166 \\ x^{}=-\sqrt[]{11}+9\longrightarrow x=-3.3166+9=5.6834 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/1l96429l801mnt2lcuswhzxeg1hi3wedm7.png)
Rounding these values for x to the nearest hundredth (2 decimal places):
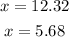
Answer:
Form:
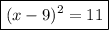
Solution: