Given: $36.52,$42.30.$39.78. $38.26. $44.39, $49.55
to find: Mean , Median and mode
soluiton:
Since, formula for mean
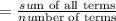
Here, sum of all terms = 36.52 + 42.30 + 39.78 + 38.26 + 44.39 + 49.55 = 250.8
number of terms = 6
Thus,
![\operatorname{mean}=(250.8)/(6)=41.8]()
Hence, mean of phone bill is $41.8
Since, number of terms = 6 which is even
so, median
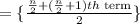
arranging the terms in ascending order: 36.52 , 38.26, 39.78, 42.30, 44.39, 49.55
Now, median
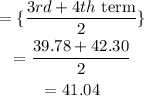
Hence, median of the phone bill is $41.04
Mode:
Given terms are 36.52 , 38.26, 39.78, 42.30, 44.39, 49.55
If no value or number in the data set appears more than once, then it has no mode
Hence, the phone bill has no mode