Question

How to find the compressive stress in a circular tube

Answer 1

Answer:

The compressive stress is 177.93 MN/m²

Explanations:

1 inch = 0.0254 meters

The outside diameter, D = 2.5 in

D = 2.5 x 0.0254

D = 0.0635 m

The inner diameter, d = 1.5 in

d = 1.5 x 0.0254

d = 0.0381 m

The area of circular tube is calculated as:

`\begin{gathered} A\text{ = }\frac{\pi{}}{4}(D^2-d^2) \\ A\text{ = }(3.142)/(4)(0.0635^2-0.0381^2) \\ A\text{ = }0.002m^2 \end{gathered}`

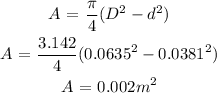
The Area of the circular tube = 0.002 m²

The compressive load = 80 kips

1 kips = 4448.22 N

The compressive load = 4448.22 x 80 N

The compressive load = 355857.6N

`\begin{gathered} \text{Compressive stress = }\frac{Compressive\text{ load}}{\text{Area}} \\ \text{Compressive stress = }(355857.6)/(0.002) \\ \text{Compressive stress = }177928800N/m^2 \\ \text{Compressive stress = }177.93MN/m^2 \end{gathered}`