The figure given in the question is a composite figure, meaning that it comprises two different figures
The volume of the composite figure can be found as follow
The two figures are:
Cylinder and sphere.
To solve this, we will first find the area of a cylinder
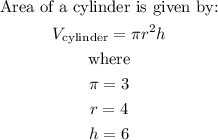
So, we will have
![\begin{gathered} V_{\text{cylinder}}=3*4^2*6 \\ V_{\text{cylinder}}=288\operatorname{cm}^3 \end{gathered}]()
Then, we will find the volume of the sphere
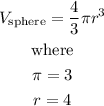
Thus, the volume of the sphere will be
![\begin{gathered} V_{\text{sphere}}=(4)/(3)*3*4^3 \\ V_{\text{sphere}}=256\operatorname{cm}^3 \end{gathered}]()
Thus, the total volume will be
![288+256=544\operatorname{cm}^3]()
The volume is:
![544\operatorname{cm}^3]()
The answer is 544cm³