1 Answer

Jagough · Answer 1 · 2023-04-25T20:23:01+0000

The figure given in the question is a composite figure, meaning that it comprises two different figures

The volume of the composite figure can be found as follow

The two figures are:

Cylinder and sphere.

To solve this, we will first find the area of a cylinder

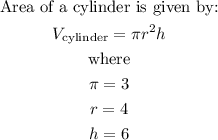
$\begin{gathered} \text{Area of a cylinder is given by:} \\ V_{\text{cylinder}}=\pi r^2h \\ \text{where} \\ \pi=3 \\ r=4 \\ h=6 \end{gathered}$

So, we will have

$\begin{gathered} V_{\text{cylinder}}=3*4^2*6 \\ V_{\text{cylinder}}=288\operatorname{cm}^3 \end{gathered}$

Then, we will find the volume of the sphere

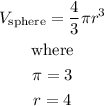
$\begin{gathered} V_{\text{sphere}}=(4)/(3)\pi r^3 \\ \text{where} \\ \pi=3 \\ r=4 \end{gathered}$

Thus, the volume of the sphere will be

$\begin{gathered} V_{\text{sphere}}=(4)/(3)*3*4^3 \\ V_{\text{sphere}}=256\operatorname{cm}^3 \end{gathered}$

Thus, the total volume will be

$288+256=544\operatorname{cm}^3$

The volume is:

$544\operatorname{cm}^3$

The answer is 544cm³

Please log in or register to add a comment.