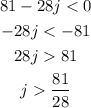The discriminant of a quadratic equation tells us whether there are two solutions, one solution or no real solutions and it is described as the part inside the root
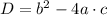
the conditions are:
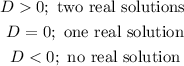
give values to a, b, and c, which are 7, 9, and j respectively.
using the third condition find the values for j that make the quadratic equation have no solution
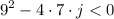
solve the inequality