Question

Find all values of j for which the quadratic equation has no real solutions.7x^2+9x+j=0Write your answer as an equality or inequality in terms of j.

Answer 1

The discriminant of a quadratic equation tells us whether there are two solutions, one solution or no real solutions and it is described as the part inside the root

`D=b^2-4a\cdot c`

the conditions are:

`\begin{gathered} D>0;\text{ two real solutions } \\ D=0;\text{ one real solution} \\ D<0;\text{ no real solution} \end{gathered}`

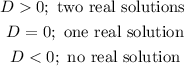
give values to a, b, and c, which are 7, 9, and j respectively.

using the third condition find the values for j that make the quadratic equation have no solution

`\begin{gathered} 9^2-4\cdot7\cdot j<0 \\ \end{gathered}`

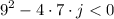
solve the inequality

`\begin{gathered} 81-28j<0 \\ -28j<-81 \\ 28j>81 \\ j>(81)/(28) \end{gathered}`