To get the volume of a prims, we do the products of the base times its height.
Being a rectangular prims, the area of its base is the product of its dimesions, so the volume of a rectangular prism is simply the product of its three dimensions:
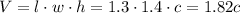
Since the volume is equal to 0.728 yd³, we have:
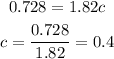
So, the measure of c is 0.4 yards.