Question

Consider the function f(x) = 5 - 4x ^ 2, - 5 <= x <= 1 .

Answer 1

Given: A function-

`f(x)=5-4x^2,\text{ }-5\leq x\leq1`

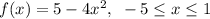
Required: To determine the absolute maxima and minima of the function.

Explanation: The given function is-

`f(x)=5-4x^2`

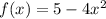
Differentiating the function,

`f^(\prime)(x)=-8x`

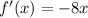
Setting f'(x)=0 gives-

`\begin{gathered} -8x=0 \\ \Rightarrow x=0 \end{gathered}`

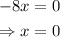
So we have to check the function at the boundary points of the interval [-5,1] and x=0 as follows-

Hence, the absolute maximum is 5 at x=o, and the minimum is -95 at x=-5.

Final Answer: The absolute maximum value is 5, and this occurs at x=0.

The absolute minimum value is -95, and this occurs at x=-5.