Answer:
To find the area of the polygon with vertices C(5, 3), A(8, -2), S(3, -4), and H(0, -2).
We have that formula for finding the area of the parallelogram with n vertices is,
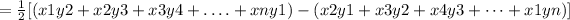
we get that,
Area of the polygon with 4 vertices that is (x1,y1),(x2,y2),(x3,y3) and (x4,y4) is
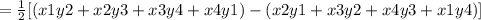
Substituting the values we get,
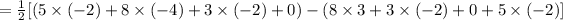
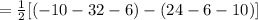
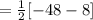
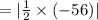
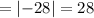
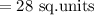
An