Question

Given A(2,4) and B(5,-4) from problem #1. What is the slope of a line that is parallel to (AB) ⃡?What is the slope of a line that is perpendicular to (AB) ⃡?

Answer 1

Given that

`\begin{gathered} A(2,4) \\ B(5,-4) \end{gathered}`

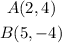
To find the slope, m, of the line passing through the given points, the formula is

`m=(y_2-y_1)/(x_2-x_1)`

Where

`\begin{gathered} (x_1,y_1)\Rightarrow A(2,4) \\ (x_2,y_2)\Rightarrow B(5,-4) \end{gathered}`

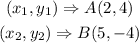
Substitute the coordinates into the formula to find the slope, m, of a line

`\begin{gathered} m=(y_2-y_1)/(x_2-x_1) \\ m=(-4-4)/(5-2)=(-8)/(3)=-(8)/(3) \\ m=-(8)/(3) \end{gathered}`

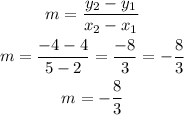
The slope of the line AB passing through the given points is m = -8/3

A) If two lines are parallel, their slopes are equal.

Hence, the slope, m₁ of the line that is parellel to line AB is

`m_1=-(8)/(3)`

Thus, the slope of a line parallel to line AB is m₁ = -8/3

B) If two lines are perpendicular, the formula to find the slope m₂ of the line perpedicular to the slope of a given line

`m_2=-\frac{1}{m_{}}`

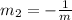
Where m = -8/3, the slope, m₂, of a line perpendicular to line AB will be

`\begin{gathered} m_2=-\frac{1}{m_{}} \\ m_2=-\frac{1}{(-8)/(3)_{}}=(3)/(8) \\ m_2=(3)/(8) \end{gathered}`

Thus, the slope of a line perpendicular to line AB is m₂ = 3/8