Answer:
All the options except the third choice are correct.
Step-by-step explanation:
In the given figure:
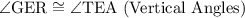
Since angles G and T are congruent:
• Triangles GER and TEA are similar triangles.
Therefore, the following holds:
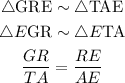
Similarly:

Finally, angles R and A are congruent.
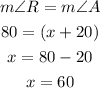
The correct choices are:
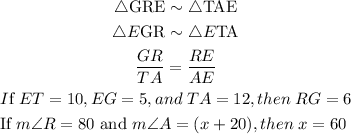
Only the third choice is Incorrect.