To find this area, it is necessary to solve an integral, actually the sum of 2 integrals
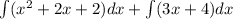
The first one must be evaluated from -3 to 2 and the second one from 2 to 3
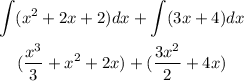
Evaluate the first integral
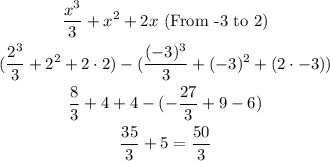
Evaluate the second integral
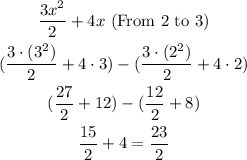
Now, solve the sum
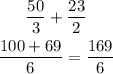
The area is 169/6