SOLUTION
Step 1 :
In this equation, we are expected to find the x-intercept(s)
of the vertex and the co-ordinates of the vertex of the parabola :
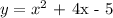
Step 2 :
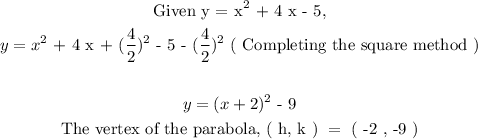
Step 3 :
We need to solve for the x-intercepts,
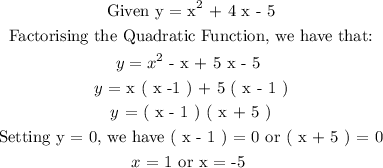
CONCLUSION:
The vertex of the parabola, ( h, k ) = ( -2 , -9 )
The x - intercepts are : x = 1 or x = -5