Question

Find the x-intercept(s) and the coordinates of the vertex for the parabola y=x² + 4x - 5. If there is more than one x-Intercept, separate them with commas.DD:x-intercept(s):5?vertex:00

Answer 1

Step 1 :

In this equation, we are expected to find the x-intercept(s)

of the vertex and the co-ordinates of the vertex of the parabola :

`y=x^2\text{ + 4x - 5}`

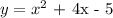
Step 2 :

`\begin{gathered} \text{Given y = x}^2\text{ + 4 x - 5,} \\ y=x^2\text{ + 4 x + (}(4)/(2))^2\text{ - 5 - (}(4)/(2))^2\text{ ( Completing the square method )} \\ \\ y=(x+2)^2\text{ - }9 \\ \text{The vertex of the parabola, ( h, k ) }=\text{ ( -2 , -9 )} \end{gathered}`

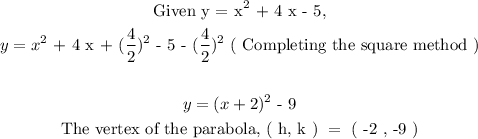
Step 3 :

We need to solve for the x-intercepts,

`\begin{gathered} \text{Given y = x}^2\text{ + 4 x - 5} \\ \text{Factorising the Quadratic Function, we have that:} \\ y=x^2\text{ - x + 5 x - 5 } \\ y\text{ = x ( x -1 ) + 5 ( x - 1 )} \\ y\text{ = ( x - 1 ) ( x + 5 )} \\ \text{Setting y = 0, we have ( x - 1 ) = 0 or ( x + 5 ) = 0} \\ x\text{ = 1 or x = -}5\text{ } \end{gathered}`

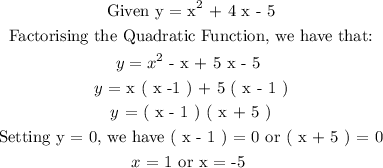
CONCLUSION:

The vertex of the parabola, ( h, k ) = ( -2 , -9 )

The x - intercepts are : x = 1 or x = -5