Question

Please help me with this problem I am trying to help my son to understand I have attached what I have helped him with so far just need to be sure i am correct:Solve the system of equations.13x−y=90y=x^2−x−42 Enter your answers in the boxes. ( __,__) and (__,__)

Answer 1

y=xTo solve the system of equations, follow the steps below.

Step 01: Substitute the value of y from equation 2 in equation 1.

In the second equation:

`y=x^2-x-42`

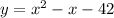
In the first equation:

`13x-y=90`

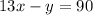
So, let's substitute y by x² - x - 42.

`\begin{gathered} 13x-y=90 \\ 13x-(x^2-x-42)=90 \\ 13x-x^2+x+42=90 \end{gathered}`

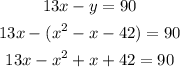
Adding the like terms:

`-x^2+14x+42=90`

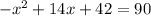
Subtracting 90 from both sides:

`\begin{gathered} -x^2+14x+42-90=90-90 \\ -x^2+14x-48=0 \end{gathered}`

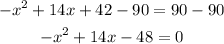
Step 02: Use the quadratic formula to solve the equation.

For a quadratic equation ax² + bx + c = 0, the quadratic formula is:

`\begin{gathered} x=(-b\pm√(b^2-4ac))/(2a) \\ \end{gathered}`

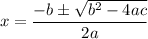
In this question, the equation is -1x² + 14x + -48 = 0, then, teh coeffitients are:

a = -1

b = 14

c = -48

Substituting the values and solving the equation:

`\begin{gathered} x=(-14\pm√(14^2-4*(-1)*(-48)))/(2*(-1)) \\ x=(-14\pm√(196-192))/(-2) \\ x=(-14\pm√(4))/(-2)=(-14\pm2)/(-2) \\ x_1=(-14-2)/(-2)=(-16)/(-2)=8 \\ x_2=(-14+2)/(-2)=(-12)/(-2)=6 \end{gathered}`

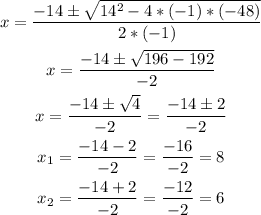
Step 03: Substitute the values of x in one equation and find y.

Knowing that:

`y=x^2-x-42`

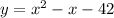
Let's substitute x by 6 and 8 and find the ordered pairs that are the solution of the system.

First, for x = 8:

`\begin{gathered} y=8^2-8-42 \\ y=64-8-42 \\ y=14 \end{gathered}`

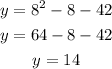
Second, for x = 6:

`\begin{gathered} y=6^2-6-42 \\ y=36-48 \\ y=-12 \end{gathered}`

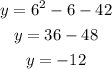
So, the solutions for the system of equations are (8, 14) and (6, -12).

Answer: (8, 14) and (6, -12).