y=xTo solve the system of equations, follow the steps below.
Step 01: Substitute the value of y from equation 2 in equation 1.
In the second equation:

In the first equation:
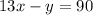
So, let's substitute y by x² - x - 42.

Adding the like terms:

Subtracting 90 from both sides:
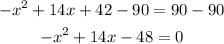
Step 02: Use the quadratic formula to solve the equation.
For a quadratic equation ax² + bx + c = 0, the quadratic formula is:
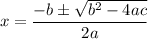
In this question, the equation is -1x² + 14x + -48 = 0, then, teh coeffitients are:
a = -1
b = 14
c = -48
Substituting the values and solving the equation:
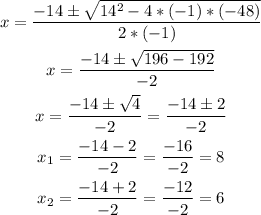
Step 03: Substitute the values of x in one equation and find y.
Knowing that:

Let's substitute x by 6 and 8 and find the ordered pairs that are the solution of the system.
First, for x = 8:
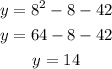
Second, for x = 6:
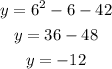
So, the solutions for the system of equations are (8, 14) and (6, -12).
Answer: (8, 14) and (6, -12).