The area of a rectangle is:
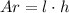
Where:
Ar = area of the rectangle
l = lenght
w = width
And the area of a triangle is:
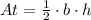
Where:
At = area of the triangle
b = base
h = height
To solve this problem divide the figure into triangles and rectangles, according to the figure below.
And the square feed (A) needed will be:
A = A1 - A2 + A3 + A4 + A5
Step 01: Calculate A1.
Figure 1 is a rectangle with sides 5 and 6 ft.
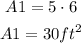
Step 02: Calculate A2.
Figure2 is a rectangle with sides 2 and 3 ft.
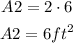
Step 03: Calculate A3.
Figure 3 is a triangle with base 4 (12 - 6 - 2 = 4) and height 3 ft.
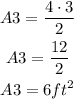
Step 04: Calculate A4.
Figure 4 is a rectangle with sides 4 (12 - 6 - 2 = 4) and 2 (5 - 3 = 2) ft.
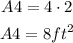
Step 05: Calculate A5.
Figure 5 is a rectangle with sides 2 and 5 ft.
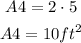
Step 06: Find the area of the figure.
A = A1 - A2 + A3 + A4 + A5.
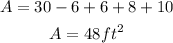
Answer: 48 ft² is needed for this hole.