Question

I've tried similar questions to this I still don't understand it also I'm not entirely sure if the top piece is correct

Answer 1

One way to make sure that the regression you made is by replacing one of the values of c, from your table and see if the predicted value that your regression gives you is close to the actual value from your table.

In this case, when we replace the first value of c (11.5) into the equation that you got from the regression, we can see that the value of p equals 13.73, which is actually close to the value reported in the table (13.8), since it is a regression it is not expected to obtain the exact value but the closest one.

If we want to find how many murders per 100000 residents we could have when c equals 8400, we just have to use the formula that you found (the regression) and calculate p, the result would be:

`p=0.829*8400+4.199=6967.799`

If we want to know the number of weapons, we just have to solve for c from the equation of the regression and replace the number of murders per 100000 residents, like this:

`\begin{gathered} p=0.829* c+4.199 \\ p-4.199=0.829* c \\ (p-4.199)/(0.829)=c \\ c=(p-4.199)/(0.829) \end{gathered}`

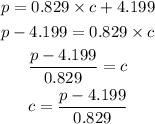
Now, we can calculate the value of c, by replacing 9.5 into p

`c=(9.5-4.199)/(0.829)=6.39`

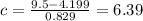
then c=6, since we have to round it to the nearest whole number