Scale factor
Initial explanation
In order to find the scale factor of the dilation of ΔABC, we just need to divide any pair of the corresponding sides of both triangles. We have that the division of the corresponding sides will be always the same:
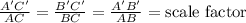
We are going to choose the first division:
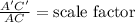
Finding the scale factor
We have that AC = 5 and A'C' = 10:
Then:
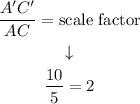
The scale factor is 2.
And since the point C and C' are the same, the center is C.
Answer- A. center C and scale factor 2