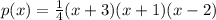Question

Third-degree, with zeros of -3,-1, and 2 and passes through the point (3,6)

Answer 1

Since the polynomial must have zeroes at x=-3, x=-1, x=2, then, we can write it as a combination of the factors (x+3), (x+1), (x-2):

`p(x)=k(x+3)(x+1)(x-2)`

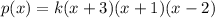
The constant k will help us to adjust the value of the polynomial when x=3:

`\begin{gathered} p(3)=k(3+3)(3+1)(3-2) \\ =k(6)(4)(1) \\ =24k \end{gathered}`

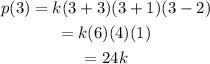
Since p(3) must be equal to 6, then:

`\begin{gathered} 24k=6 \\ \Rightarrow k=(6)/(24) \\ \Rightarrow k=(1)/(4) \end{gathered}`

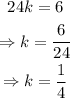
Therefore, the following polynomial function has zeroes at -3, -1 and 2, and passes through the point (3,6):

`p(x)=(1)/(4)(x+3)(x+1)(x-2)`