Question

Potassium-42 has a half-life of 12.4 hours. How much of a 746-gram sample will be left after 62 hours?

Answer 1

the amount of potassium-42 remaining after 62 hours is approximately 23.31 grams (option B)

Step-by-step explanation:

half life = 12.4 hours

initial amount = 746g

time elapsed = 62 hours

Using the half-life formula:

`\begin{gathered} N(t)=N_0((1)/(2))^{\frac{t}{t_{_{(1)/(2)}}}} \\ N(t)\text{ = amount remaining} \\ N_0\text{ = initial amount = 746g} \\ t\text{ = 62 hours} \\ t_{(1)/(2)\text{ }}\text{ = 12.4 hours} \end{gathered}`

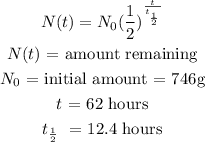
Substitute for the values:

`\begin{gathered} N(t)=N_0((1)/(2))^{\frac{t}{t_{_{(1)/(2)}}}} \\ N(t)\text{ = }746((1)/(2))^{(62)/(12.5)} \\ N(t)\text{ = }746((1)/(2))^5 \\ N(t)\text{ = }746((1)/(2^5)) \end{gathered}`
`\begin{gathered} N(t)\text{ = }((746)/(32))^{} \\ N(t)\text{ = }23.3125 \end{gathered}`

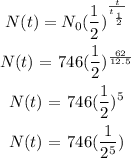
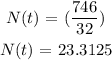
Hence, the amount of potassium-42 remaining after 62 hours is approximately 23.31 grams (option B)