Remember that the coordinates of the points are written in the form (x,y), the first entry represents the distance over the horizontal axis and the second entry represents the distance over the vertical axis.
Plot the given points on the coordinate plane:
The length of the segment UV is 4, and the length of the segment UW is 9. Since the triangle VUW is a right triangle, use the Pythagorean Theorem to find the length of the segment VW:
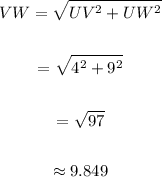
Add the lengths of all the segments to find the perimeter of the triangle:
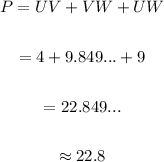
Therefore, to the nearest tenth, the perimeter of the triangle is 22.8.