Given:
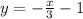
We have the graph below:
To determine the correct ordered pairs, let's solve for each of them.
a) (x, y) ==> (0, -1)
From the equation, substitute 0 for x and -1 for y:

b) (x, y) ==> (3, -2)
Substitute 3 for x and -2 for y:
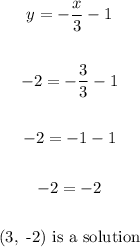
c) (x, y) ==> (3, -5)
Substitute 3 for x and -5 for y:
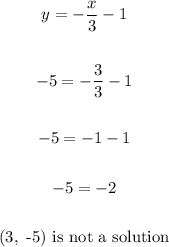
d) (0, -5)
Substitute 0 for x and -5 for y:
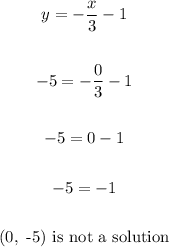
e) (x, y) ==> (-3, 0)
Substitute -3 for x and 0 for y:

ANSWER:
(0, -1)
(3, -2)
(-3, 0)