Question

Find the other endpoint of the line segment with the given endpoint and midpoint. Endpoint: (5,-1) Midpoint: (5,-4)

Answer 1

The formula for calculating the midpoint of a line segment is given below

`(x,y)=((x_1+x_2))/(2),((y_1+y_2))/(2)`

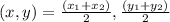
Where the values are

`\begin{gathered} x=5,y=-4 \\ x_1=5,y_1=-1 \end{gathered}`

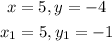
By substituting the values, we will have

`\begin{gathered} (x,y)=((x_1+x_2))/(2),((y_1+y_2))/(2) \\ (5,-4)=\frac{(5_{}+x_2)}{2},\frac{(-1_{}+y_2)}{2} \end{gathered}`

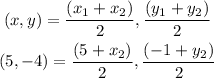
By comparing coefficient, we will have

`\begin{gathered} \frac{(5_{}+x_2)}{2}=5 \\ \frac{(-1_{}+y_2)}{2}=-4 \end{gathered}`

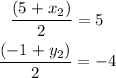
Cross multiply to get the values of x2

`\begin{gathered} \frac{(5_{}+x_2)}{2}=5 \\ 5+x_2=10 \\ \text{substract 5 from both sides} \\ 5-5+x_2=10-5 \\ x_2=5 \end{gathered}`

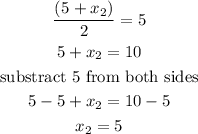
Cross multiply to get the values of y2

`\begin{gathered} \frac{(-1_{}+y_2)}{2}=-4 \\ -1+y_2=-8 \\ \text{add 1 to both sides} \\ -1+1+y_2=-8+1_{} \\ y_2=-7 \end{gathered}`

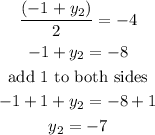
Hence,

The coordinate of the other endpoint is ( 5, -7 )