The formula for calculating the midpoint of a line segment is given below
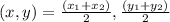
Where the values are
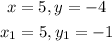
By substituting the values, we will have
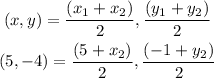
By comparing coefficient, we will have
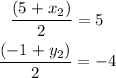
Cross multiply to get the values of x2
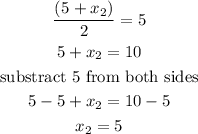
Cross multiply to get the values of y2
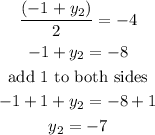
Hence,
The coordinate of the other endpoint is ( 5, -7 )