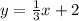Before we calculate the perpendicular line, let's rewrite our line equation in slope-intercept form. The slope-intercept form is

Where m represents the slope and b the y-intercept.
Rewritting our equation, we have
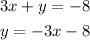
This means the slope of our line is equal to - 3.
Two perpendicular lines are related by their slope. Let's say two lines are perpendicular, this means the slope of one of the lines is equal to minus the inverse the slope of the other. If we call the slope of one of those lines as m_1, the slope of the perpendicular line m_2 is given by
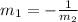
Using this relation, we can find the slope of a perpendicular line. Since the slope of our line is equal to - 3, then, the slope of the perpendicular line is
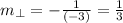
In slope-intercept form, our perpendicular line has the following form
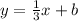
To find our y-intercept, we can use our given point that belongs to this line.
The point is (-3, 1), evaluating this point in our equation, we have
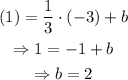
Then, our line is