Given the function:
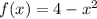
For the given function, we will determine the concavity between x = -1 and x = 5
By the average rate of change over the interval 3 ≤ x < 5
We will use the following formula:

First, we will find the value of f(5) and f(3)
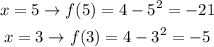
Substitute into the formula:
So, the average rate of change will be as follows:
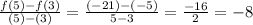
As the average rate of change is negative, the concavity of the graph will be concave down