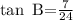To begin with, we will have to sketch the image of the question
To find the value of tan B
we will make use of the trigonometric identity

From the diagram given
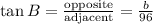
Since the value of b is unknown, we will have to get the value of b
To do so, we will use the Pythagorean theorem
![\begin{gathered} \text{hypoteuse}^2=\text{opposite}^2+\text{adjacent}^2 \\ b^2=100^2-96^2 \\ b=\sqrt[]{784} \\ b=28 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/rqblbsnzyvaw195bkpsiktvro87wxi936u.png)
Since we now know the value of b, we will then substitute this value into the tan B function
so that we will have
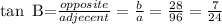
Therefore