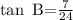Question

Suppose ABC is a right triangle of lengths a, b and c and right angle at c. Find the unknown side length using the Pythagorean theorem and then find the value of the indicated trigonometric function of the given angle. Rationalize the denominator if applicable.Find tan B when a=96 and c=100

Answer 1

To begin with, we will have to sketch the image of the question

To find the value of tan B

we will make use of the trigonometric identity

`\tan \theta=(opposite)/(adjacent)`

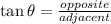
From the diagram given

`\tan B=\frac{\text{opposite}}{\text{adjacent}}=(b)/(96)`

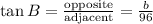
Since the value of b is unknown, we will have to get the value of b

To do so, we will use the Pythagorean theorem

`\begin{gathered} \text{hypoteuse}^2=\text{opposite}^2+\text{adjacent}^2 \\ b^2=100^2-96^2 \\ b=\sqrt[]{784} \\ b=28 \end{gathered}`

Since we now know the value of b, we will then substitute this value into the tan B function

so that we will have

`\tan \text{ B=}(opposite)/(adjecent)=(b)/(a)=(28)/(96)=(7)/(24)`

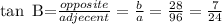
Therefore

`\tan \text{ B=}(7)/(24)`