Question

Carbon-14 is used for archeological carbon dating. Its half-life is 5730 years. How much of a 50-gram sample of Carbon-14 will be left in 1000 years?

Answer 1

Given:

The half-life of carbon-14 is 5730 years.

The initial amount of carbon is I = 50 grams.

Step-by-step explanation:

To find the final amount of carbon after 1000 years.

The fundamental decay equation is,

`\begin{gathered} F=Ie^(-\lambda t) \\ \text{Where, }\lambda=\frac{\ln 2}{t_{(1)/(2)}} \end{gathered}`

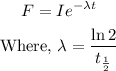
Let us find the radioactive constant first.

`\begin{gathered} \lambda=(\ln 2)/(5730) \\ \lambda=0.00012096809 \end{gathered}`

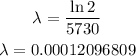
Then, the final amount of the corban-14 is,

`\begin{gathered} F=50e^(-0.000121(1000))^{} \\ =44.30g \end{gathered}`

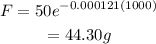
Hence, the amount of a 50-gram sample of Carbon-14 will be left in 1000 years is 44.30 g.