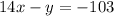Given the pair of coordinates;

We would begin by first calculating the slope of the line.
This is given by the formula;

The variables are as follows;
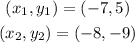
We will now substitute these into the formula for finding the slope as shown below;
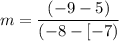
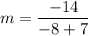
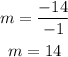
The slope of this line equals 14. We shall use this value along with a set of coordinates to now determine the y-intercept.
Using the slope-intercept form of the equation we would have;

We would now substitute for the following variables;
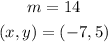
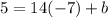
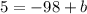
Add 98 to both sides of the equation;
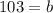
We now have the values of m, and b.The equation in "slope-intercept form" would be;
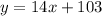
To convert this linear equation into the standard form which is;
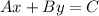
We would move the term with variable x to the left side of the equation;
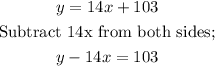
We can now re-write and we'll have;
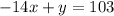
Note that the coefficients of x and y (that is A and B) are integers and A is positive;
Therefore, we would have;
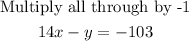
The equation of the line passing through the points given expressed in standard form is;
ANSWER: