Question

How is the series 7 + 13 + 19+...+ 139 represented in summation notation?

Answer 1

Each term is 6 greater than the previous term.

First term is "7".

So,

a = 7

d = 6

Let's find the formula for the series,

`\begin{gathered} a+(n-1)d \\ 7+(n-1)(6) \\ 7+6n-6 \\ 6n+1 \end{gathered}`

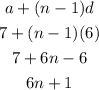
We can immediately eliminate the firsst and third choice.

The variable is "t", so the general formula will be:

`6t+1`

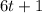
How many terms are there?

The series starts from t = 1,

since 6(1) + 1 = 6 + 1 = 7

and 6(2) + 1 = 12 + 1 = 13

The terms match!

So, 2nd answer choice is correct!!

Answer
`\sum ^(23)_(t\mathop=1)(6t+1)`