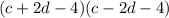INFORMATION:
We have the following expression
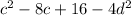
And we must factor it by grouping
STEP BY STEP EXPLANATION:
To factor it by grouping, we must:
1. group the first 3 terms of the expression
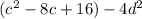
2. factor the expression in the parenthesis
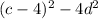
3. rewrite 4d^2 as unique exponential expression
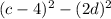
4. factor by square difference
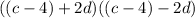
5. simplify
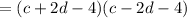
ANSWER:
the factoring for c^2-8c +16 -4d^2 by grouping is