Question

List the following information about the function: y = 2 (x-3)^2-1 (parent graph y = x^2)

Answer 1

Given

The function is defined as:

`y\text{ = 2\lparen x -3\rparen}^2\text{ - 1}`

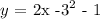
x-intercepts

The x-intercepts of the function y are the values of x when y = 0

Substituting 0 for y and solving for x

`\begin{gathered} 2(x-3)^2\text{ -1 = 0} \\ 2(x-3)^2\text{ = 1} \\ Divide\text{ both sides by 2} \\ (x-3)^2\text{ = }(1)/(2) \\ Square\text{ root both sides} \\ x-3\text{ = }\pm\sqrt{(1)/(2)} \\ x\text{ = 3 }\pm\text{ }\sqrt{(1)/(2)} \end{gathered}`

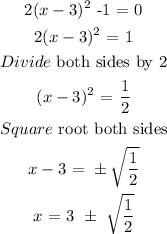
Hence, the x-intercepts are:

`(\sqrt{(1)/(2)}\text{ + 3, 0\rparen, \lparen-}\sqrt{(1)/(2)}\text{ + 3,0\rparen}`

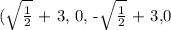
y-intercepts

The y-intercepts are the values of y when x = 0

`\begin{gathered} y\text{ = 2\lparen0-3\rparen}^2-\text{ 1} \\ =\text{ 2}*9-1 \\ =\text{ 17} \end{gathered}`

Hence, the y-intercept is (0, 17)

Maximum or minimum of the function

The given equation is in vertex form.

`\begin{gathered} y\text{ = a\lparen x-h\rparen}^2\text{ + k} \\ Where\text{ \lparen h,k\rparen is the vertex} \end{gathered}`

Hence, the minimum value of the function is (3,-1)