Question

I tried everything I could to answer this question but I couldn’t get it

Answer 1

We need to use some properties of the kyte:

· The opposite obtuse angles are equal. In the figure, this means ∠WZY = ∠WXY

· The large diagonal bisects the angles ∠ZWX and ∠XYZ

56 ask us to find m∠XYZ. We can note that the angles ∠ZXY and ∠XZY are congruent. And we know that the interior angles of the triangle XYZ add to 180º.

m∠VXY = m∠VZY = 58º

Then:

`\begin{gathered} m∠ZXY+m∠XZY+m∠XYZ=180º \\ 58º+58º+m∠XYZ=180º \\ m∠XYZ=64º \end{gathered}`

The answer to 56. is 64º

57 ask us to find m∠ZWV, we can use the second property listed above. The large diagonal bisects the angle ∠ZWX. Since we know ∠ZWX = 50º, then:

`\begin{gathered} m∠ZWV=(1)/(2)\cdot m∠ZWX \\ . \\ m∠ZWV=(1)/(2)\cdot50º=25º \end{gathered}`

The answer to 57 is 25º

58 ask us to find m∠VZW. We know that the sum of all internal angles of a kite (or any quadrilateral), is 360º.

We know:

m∠ZWX = 50º

m∠WZY = m∠WXY

m∠XYZ = 64º

Then:

`\begin{gathered} m∠ZWX+m∠WZY+m∠WXY+m∠XYZ=360º \\ 50º+2m∠WZY+64º=360º \\ 2m∠WZY=360º-114º \\ m∠WZY=(1)/(2)\cdot246º \\ m∠WZY=123º \end{gathered}`

And:

`m∠WZY=m∠VZW+m∠VZY`

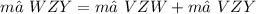
Now replace the known values of m∠WZY = 123º and m∠VZY = 58º:

`\begin{gathered} 123º=m∠VZW+58º \\ m∠VZW=123º-58º=65º \end{gathered}`

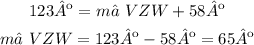
The answer to 58 is 65º

59 ask us to find m∠WZY, we sis it in 58 to find m∠VZW.

The answer to 59 is 123º