Question

Find the center that eliminates the linear terms in the translation of 4x^2 - y^2 + 24x + 4y + 28 = 0.(-3, 2)(-3,- 2)(4, 0)

Answer 1

Step 1

Given;

`4x^2-y^2+24x+4y+28=0`

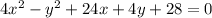
Required; To find the center that eliminates the linear terms

Step 2

`\begin{gathered} 4x^2-y^2+24x+4y=-28 \\ 4x^2+24x-y^2+4y=-28 \\ Complete\text{ the square }; \\ 4x^2+24x \\ \text{use the form ax}^2+bx\text{ +c} \\ \text{where} \\ a=4 \\ b=24 \\ c=0 \end{gathered}`
`\begin{gathered} consider\text{ the vertex }form\text{ of a }parabola \\ a(x+d)^2+e \\ d=(b)/(2a) \\ d=(24)/(2*4) \\ d=(24)/(8) \\ d=3 \end{gathered}`
`\begin{gathered} Find\text{ the value of e using }e=c-(b^2)/(4a) \\ e=0-(24^2)/(4*4) \\ e=0-(576)/(16)=-36 \end{gathered}`

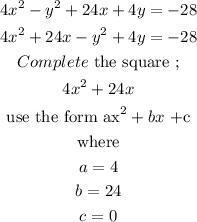
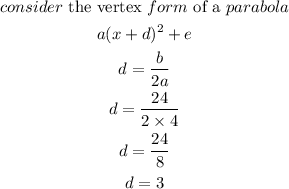
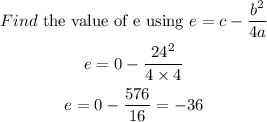
Step 3

Substitute a,d,e into the vertex form

`\begin{gathered} a(x+d)^2+e \\ 4(x+_{}3)^2-36 \end{gathered}`
`\begin{gathered} 4(x+3)^2-36-y^2+4y=-28 \\ 4(x+3)^2-y^2+4y=\text{ -28+36} \\ \\ \end{gathered}`

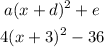
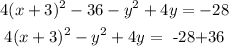
Step 4

Completing the square for -y²+4y

`\begin{gathered} \text{use the form ax}^2+bx\text{ +c} \\ \text{where} \\ a=-1 \\ b=4 \\ c=0 \end{gathered}`
`\begin{gathered} consider\text{ the vertex }form\text{ of a }parabola \\ a(x+d)^2+e \\ d=(b)/(2a) \\ d=\text{ }(4)/(2*-1) \\ d=(4)/(-2) \\ d=-2 \end{gathered}`
`\begin{gathered} Find\text{ the value of e using }e=c-(b^2)/(4a) \\ e=0-(4^2)/(4*(-1)) \\ \\ e=0-(16)/(-4) \\ e=4 \end{gathered}`

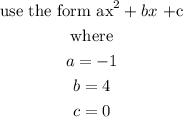
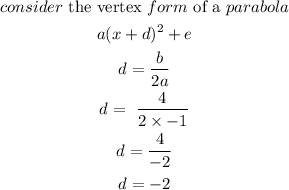
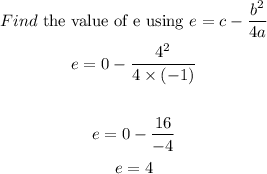
Step 5

Substitute a,d,e into the vertex form

`\begin{gathered} a(y+d)^2+e \\ =-1(y+(-2))^2+4 \\ =-(y-2)^2+4 \end{gathered}`

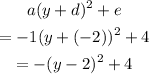
Step 6

`\begin{gathered} 4(x+3)^2-y^2+4y=\text{ -28+36} \\ 4(x+3)^2-(y-2)^2+4=-28+36 \\ 4(x+3)^2-(y-2)^2=-28+36-4 \\ 4(x+3)^2-(y-2)^2=4 \\ (4(x+3)^2)/(4)-((y-2)^2)/(4)=(4)/(4) \\ (x+3)^2-((y-2)^2)/(2^2)=1 \end{gathered}`

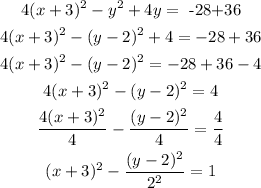
Step 7

`\begin{gathered} ((x-h)^2)/(a^2)-((y-k)^2)/(b^2)=1 \\ \text{This is the }form\text{ of a hyperbola.} \\ \text{From here } \\ a=1 \\ b=2 \\ k=2 \\ h=-3 \end{gathered}`

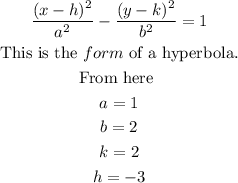
Hence the answer is (-3,2)