Question

Find the range and standard deviation of the set of data.230, 232, 234, 236, 238, 240, 242

Answer 1

The data given is ,230, 232, 234, 236, 238, 240, 242.

The range of the data is defined the difference of largest number from smallest number.

The largest number in the data is, 242.

The smallest number in the data is, 230.

Therefore, the range is determined as

`R=242-230`
`R=12.`

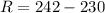
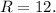
The range of the set of data is 12.

To determine the standard deviation,

First determine the mean of the data,

`E(x)=(230+232+234+236+238+240+242)/(7)`
`E(x)=(1652)/(7)`
`E(x)=236`

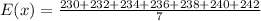
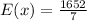
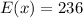
The value of

`E(x^2)=(230-236)^2+(232-236)^2+(234-236)^2+(236-236)^2+(238-236)^2+(240-236)^2+(242-236)^2`

`E(x^2)=36+16+4+0+4+16+36`
`E(x^2)=112`

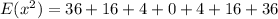
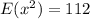
The standard deviation is determined as,

`SD=\sqrt[]{v}`

Here v denotes the variance.

`v=(112)/(7-1)`
`v=(112)/(6)`
`v=18.66`

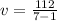
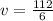
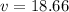
The standard deviation is given as,

`SD=\sqrt[]{18.66}`
`SD=4.32`