Given:
The radius of the circular disk is 24cm.
The radius has a maximum error of 0.2 cm.
To find:
The area
Step-by-step explanation:
Using the area of the circle,
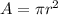
The area of the disk is,
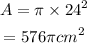
If the radius is increased from 24 by 0.02, then the radius becomes, r = 0.02
The change in the calculated area will be,
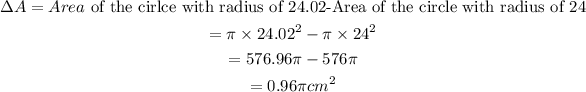
The relative percentage of area is,
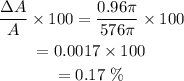
Final answer:
The maximum error in area is,
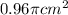
The relative percentage error in the area is 0.17%.