Question

(linear approximation calc !) The radius of a disc is 24 cm if the radius has a maximum error of 0.2 cm. estimate the relative percentage air in the calculated area the area of a circle = pi r ^2

Answer 1

Given:

The radius of the circular disk is 24cm.

The radius has a maximum error of 0.2 cm.

To find:

The area

Step-by-step explanation:

Using the area of the circle,

`A=\pi r^2`

The area of the disk is,

`\begin{gathered} A=\pi*24^2 \\ =576\pi cm^2 \end{gathered}`

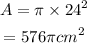
If the radius is increased from 24 by 0.02, then the radius becomes, r = 0.02

The change in the calculated area will be,

`\begin{gathered} \Delta A=Area\text{ of the cirlce with radius of 24.02-Area of the circle with radius of 24} \\ =\pi*24.02^2-\pi*24^2 \\ =576.96\pi-576\pi \\ =0.96\pi cm^2 \end{gathered}`

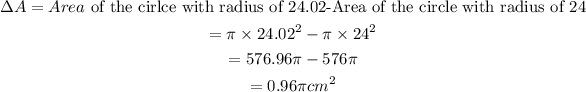
The relative percentage of area is,

`\begin{gathered} (\Delta A)/(A)*100=(0.96\pi)/(576\pi)*100 \\ =0.0017*100 \\ =0.17\text{ \%} \end{gathered}`

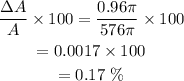
Final answer:

The maximum error in area is,

`0.96\pi cm^2`

The relative percentage error in the area is 0.17%.