ANSWER
0.1069
Step-by-step explanation
We have two possible outcomes for each experiment: the seed grows or the seed does not grow. So, this follows a binomial distribution, where, in this case, the probability of success is the probability that a seed does not grow - note that we want to find what is the probability that a number of seeds do not grow.
We know that the probability that a seed grows is 85%, so there is a 15% chance the seed does not grow. This experiment is repeated 9 times (9 seeds) and we want to find what is the probability that the number of successes is 3 - remember that "success" is that the seed doesn't grow.
To find this, we have to use the binomial probability formula,
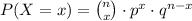
For this problem:
• n = 9
,
• x = 3
,
• p = 0.15
,
• q = 0.85
So we have,
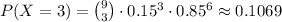
Hence, the probability that exactly 3 seeds don't grow is 0.1069, rounded to four decimal places.