Question

2x + 2/3y= -2 x, y intercept

Answer 1

We need to find the points at which the expression below intercept the axis of the coordinate plane:

`2x+(2)/(3)y=-2`

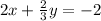
To find the "x" intercept we need to find the value of "x" that results in a value of "y" equal to 0. We have:

`\begin{gathered} 2x+(2)/(3)\cdot0=-2 \\ 2x+0=-2 \\ 2x=-2 \\ x=(-2)/(2)=-1 \end{gathered}`

To find the "y" intercept we need to find which value of "y" the function outputs when we make x equal to 0.

`\begin{gathered} 2\cdot0+(2)/(3)y=-2 \\ (2)/(3)y=-2 \\ 2y=-6 \\ y=(-6)/(2)=-3 \end{gathered}`

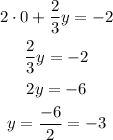
The x intercept is -1 and the y intercept is -3.