We need to find the points at which the expression below intercept the axis of the coordinate plane:
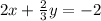
To find the "x" intercept we need to find the value of "x" that results in a value of "y" equal to 0. We have:
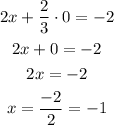
To find the "y" intercept we need to find which value of "y" the function outputs when we make x equal to 0.
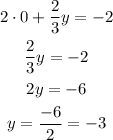
The x intercept is -1 and the y intercept is -3.