Given: Graph of a function f(x) is provided.
Required: To find the inverse of the function

Explanation: The inverse of a function is determined by interchanging the domain and the range. The domain is the input values, and the range is the output values where the function is defined.
Hence, to find the inverse of the function at x=-1, we need to look at the graph and find out at which value of x, the value of f(x), is -1. Since if
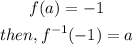
Hence we need to look at which point on the x-axis of the given function we have f(x)=-1. This is the point (-3,-1) as
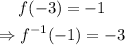
Hence the point corresponding to the inverse is (-1,-3). The point is shown below in the graph-
Final Answer: The point corresponding to the inverse of f at x=-1 is (-1,-3).