Question

Seven years ago, Tom bought a house for $80,000, whichappreciated in value at 9% per year due to inflation. If Tomhas 48 more monthly payments of $500 to make to the bankon his 12% mortgage, find his present equity in the house.

Answer 1

The equity will be the value of the house today minus the present value of the remaining mortgage payments.

We can start with the value of the house. If the house was originally valued in $80,000 and appreciated at 9% per year during 7 seven years, we can calculate the present value as:

`\begin{gathered} PV=80000\cdot(1+0.09)^7 \\ PV=80000\cdot1.09^7 \\ PV\approx80000\cdot1.828 \\ PV\approx146243.13 \end{gathered}`

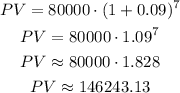
Now we can calculate the present value of the mortgage payments as an annuity.

The payments are monthly (m = 12), with an annual rate of 12% (r = 0.12). The amount paid monthly is $500 and there are 48 remaining payments (m*t = 48), so we can calculate the annuity as:

`\begin{gathered} PV=M\cdot(1-(1+(r)/(m))^(-m\cdot t))/((r)/(m)) \\ PV=500\cdot(1-(1+(0.12)/(12))^(-48))/((0.12)/(12)) \\ PV=500\cdot(1-(1.01)^(-48))/(0.01) \\ PV\approx500\cdot(1-0.62026)/(0.01) \\ PV\approx500\cdot(0.37974)/(0.01) \\ PV\approx500\cdot37.974 \\ PV\approx18986.98 \end{gathered}`

Then, if we substract the mortgage present value from the present value of the house, we get the equity:

`\begin{gathered} E=PV_{h\text{ouse}}-PV_{\text{mortgage}} \\ E=146243.13-18986.98 \\ E=127256.15 \end{gathered}`

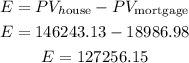
Answer: the present equity in the house is $127,256.15