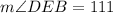Question

Line AB is perpendicular to line AC, line CD is congruent to line CE and measurement of angle B is 48° find measurement of angle DEB

Answer 1

The sum of the interior angles of a triangle adds up to 180°.

Based on this, we can do the following...

0. Finding m∠C:

`m\angle C+m\angle B+m\angle A=180`
`m\angle C=180-m\angle B-m\angle A`

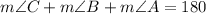
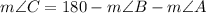
With the description of the problem, we know that m∠B = 48° and m∠A = 90°. Replacing these values:

`m\angle C=180-48-90`
`m\angle C=42`

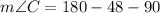
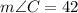
With this angle and based on the same logic that the addition of the interior angles of a circle adds up 180°, we can get m∠CED. Also, as CD is congruent to CE, m∠CED = m∠CDE.

`m\angle C+m\angle CED+m\angle CDE=180`
`m\angle C+m\angle CED+m\angle CED=180`
`m\angle C+2m\angle CED=180`
`m\angle CED=((180-m\angle C))/(2)`

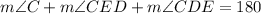
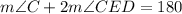
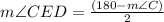
Replacing the value of m∠C previously calculated:

`m\angle CED=((180-42))/(2)=(138)/(2)`
`m\angle CED=69`

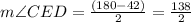
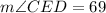
Finally, as we know segment CB is a straight line, the angle is 180°. Thus...

`m\angle DEB+m\angle CED=180`
`m\angle DEB=180-m\angle CED`

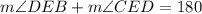
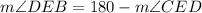
Replacing the value previously calculated:

`m\angle DEB=180-69`

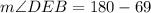
Answer:

`m\angle DEB=111`