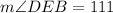The sum of the interior angles of a triangle adds up to 180°.
Based on this, we can do the following...
0. Finding m∠C:

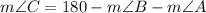
With the description of the problem, we know that m∠B = 48° and m∠A = 90°. Replacing these values:
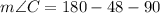
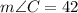
With this angle and based on the same logic that the addition of the interior angles of a circle adds up 180°, we can get m∠CED. Also, as CD is congruent to CE, m∠CED = m∠CDE.
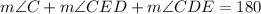
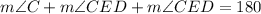
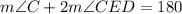
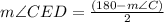
Replacing the value of m∠C previously calculated:
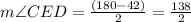
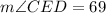
Finally, as we know segment CB is a straight line, the angle is 180°. Thus...
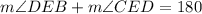
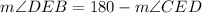
Replacing the value previously calculated:
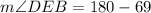
Answer: