Question

Jane has a pre-paid cell phone with A Fee and Fee. She can't remember the exact costs, but her plan has a monthly fee and a charge for each minute of calling time. In June she used 430 minutes and the cost was $227.50. In July she used 780 minutes and the cost was $385.00.

Answer 1

Given:

the plan of the pre-paid cell phone

The plan has a monthly fee and a charge for each minute

Let the monthly cost = C

and the number of minutes = x

the general equation will be:

C = ax + b

Where (b) is the monthly fee, and (a) is the charge per minute

We will find the values of (a) and (b) using the following:

1) 430 minutes cost $227.50

2) 780 minutes cost $385.00.

So, we have the following equations:

`\begin{gathered} 430a+b=227.5\rightarrow(1) \\ 780a+b=385\rightarrow(2) \end{gathered}`

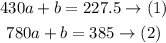
Solve the equations, subtract equation (1) from (2) to eliminate (b), and solve for (a):

`\begin{gathered} 780a-430a=385-227.5 \\ 350a=157.5 \\ a=(157.5)/(350)=0.45 \end{gathered}`

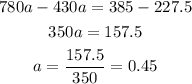
Substitute with (a) into equation (1) to find the value of (b)

`\begin{gathered} 430\cdot0.45+b=227.5 \\ 193.5+b=227.5 \\ b=227.5-193.5=34 \end{gathered}`

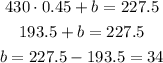
So, the equation of the monthly cost will be:

`C=0.45x+34`

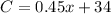
Part (b): When x = 484 minutes, we will find C

so, substitute with (x) into the equation of C

`\begin{gathered} C=0.45*484+34 \\ C=217.8+34 \\ C=251.8 \end{gathered}`

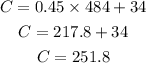
So, the answer will be:

A) C = 0.45x + 34

B) $251.8